Ok, Pearson criteria may be used for any distribution you like, but most popular is normal
theory from book “Econometrics” of Kochetkov and Tolokonnikov
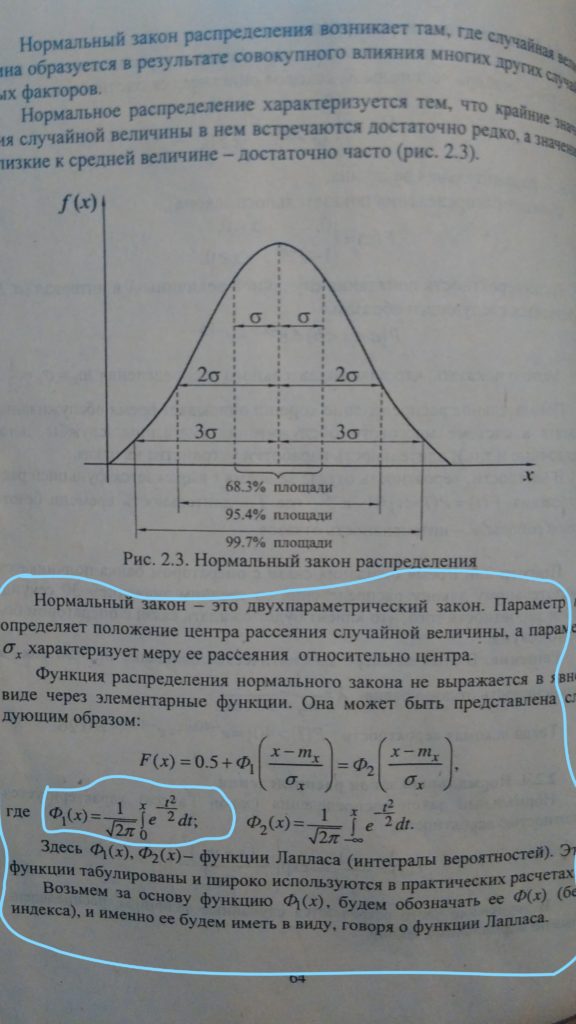 Pearson criteria will help to understand if distribution in normal?
Pearson criteria will help to understand if distribution in normal?
Below is example of testing…
Ok, this is the theory, lets write the algo which will answer the question – is distribution normal using Pearson Criteria ?
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 |
class function TMyMath.isDistributionNormal(AValues: TArray<double>; var aFreedomCount: integer; var percentile, chiSquare, chiSquareTable: extended): Boolean; var m: Integer; // count intervals n: integer; // how much el. in one interval i: integer; // cursor step: double; first, last: double; l, r: double; // borders intervals: TArray<Tinterval>; j: Integer; // counter mx: double; stdDeviaton: Double; // chiSquare: double; tF: Double; // theoretical frequency k: integer; // number of freedom power laplasRight, laplasLeft: double; qantilesSL: TStringList; percentiles: TArray<string>; chiSquareValuesTableArray: TArray<string>; begin result := false; Tarray.Sort<double>(AValues); // sort first try if Length(AValues) < 500 then // number of intervals could be improved here m := 500 div 20 else m := 30; // initial values SetLength(intervals, m); i := 0; first := AValues[0]; last := AValues[high(AValues)]; step := (last - first) / m; for j := 1 to m do begin n := 0; // number of elements in interval l := first + (j - 1) * step; // left border of interval r := first + j * step; // right border while (AValues[i] < r) and (i < Length(AValues)) do begin Inc(n); Inc(i); end; intervals[j - 1].Count := n; intervals[j - 1].Left := l; intervals[j - 1].Right := r; intervals[j - 1].Middle := (l + r) / 2; intervals[j - 1].Frequency := n; //n / Length(AValues); end; //count Mx mx := 0; for i := 0 to m - 1 do mx := mx + (intervals[i].Frequency * intervals[i].Middle) / length(AValues); //count SigmaX = standart deviation stdDeviaton := 0.00; stdDeviaton := StdDev(AValues); //count theoretical frequency and count chiSquare chiSquare := 0.00; for i := 0 to m - 1 do begin // theoretical frequency laplasRight := Laplas((intervals[i].Right - mx) / stdDeviaton); laplasLeft := Laplas((intervals[i].Left - mx) / stdDeviaton); tf := Length(AValues) * (laplasRight - laplasLeft); if tf <> 0 then chiSquare := chiSquare + (Power((intervals[i].Frequency - tf), 2) / tf); end; //compare to chiSquareTable and make conclusion k := m - 1; // number of freedom power aFreedomCount := k; // http://www.machinelearning.ru/wiki/index.php?title=%D0%9A%D1%80%D0%B8%D1%82%D0%B5%D1%80%D0%B8%D0%B9_%D1%85%D0%B8-%D0%BA%D0%B2%D0%B0%D0%B4%D1%80%D0%B0%D1%82 chiSquareTable := -1; // default values percentile := -1; qantilesSL := TStringList.Create; try createQuantiles(qantilesSL); // parse percentiles percentiles := qantilesSL[0].Split([';']); if k <= qantilesSL.Count - 1 then begin // parse chiSquareTable chiSquareValuesTableArray := qantilesSL[k].Split([';']); for i := High(chiSquareValuesTableArray) downto Low(chiSquareValuesTableArray) do // trying get appropriate percentile begin if chiSquare < chiSquareValuesTableArray[i].ToDouble() then begin result := true; percentile := percentiles[i].ToDouble(); // percentile at which distribution is normal! chiSquareTable := chiSquareValuesTableArray[i].ToDouble(); Exit; end; end; end; finally qantilesSL.Free(); end; except result := false; chiSquareTable := -1; // default values chiSquare := -1; percentile := -1; end; end; |
if needed approximation by params…
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 |
class function TMyMath.isDistributionNormal(AValues: TArray<double>; aNIntervals: Integer; var aFreedomCount: integer; var percentile, chiSquare, chiSquareTable: extended): Boolean; var // m: Integer; // count intervals n: integer; // how much el. in one interval i: integer; // cursor step: extended; first, last: extended; l, r: extended; // borders intervals: TArray<Tinterval>; j: Integer; // counter mx: extended; stdDeviaton: extended; // chiSquare: double; tF: Double; // theoretical frequency k: integer; // number of freedom power laplasRight, laplasLeft: extended; qantilesSL: TStringList; percentiles: TArray<string>; chiSquareValuesTableArray: TArray<string>; begin result := false; Tarray.Sort<double>(AValues); // sort first try // initial values SetLength(intervals, aNIntervals); i := 0; // cursor first := AValues[0]; last := AValues[high(AValues)]; step := (last - first) / aNIntervals; for j := 1 to aNIntervals do begin n := 0; // number of elements in interval l := first + (j - 1) * step; // left border of interval r := first + j * step; // right border while (AValues[i] < r) and (i < Length(AValues)) do begin Inc(n); Inc(i); end; intervals[j - 1].Count := n; intervals[j - 1].Left := l; intervals[j - 1].Right := r; intervals[j - 1].Middle := (l + r) / 2; intervals[j - 1].Frequency := n; //n / Length(AValues); end; //count Mx mx := 0; for i := 0 to aNIntervals - 1 do mx := mx + (intervals[i].Frequency * intervals[i].Middle) / length(AValues); //count SigmaX = standart deviation stdDeviaton := 0; stdDeviaton := StdDev(AValues); //count theoretical frequency and count chiSquare chiSquare := 0.00; laplasRight := 0; laplasLeft := 0; for i := 0 to aNIntervals - 1 do begin // theoretical frequency laplasRight := Laplas((intervals[i].Right - mx) / stdDeviaton); laplasLeft := Laplas((intervals[i].Left - mx) / stdDeviaton); tf := Length(AValues) * (laplasRight - laplasLeft); if tf <> 0 then chiSquare := chiSquare + (Power((intervals[i].Frequency - tf), 2) / tf); end; //compare to chiSquareTable and make conclusion k := aNIntervals - 1; // number of freedom power aFreedomCount := k; // http://www.machinelearning.ru/wiki/index.php?title=%D0%9A%D1%80%D0%B8%D1%82%D0%B5%D1%80%D0%B8%D0%B9_%D1%85%D0%B8-%D0%BA%D0%B2%D0%B0%D0%B4%D1%80%D0%B0%D1%82 chiSquareTable := -1; // default values percentile := -1; qantilesSL := TStringList.Create; try createQuantiles(qantilesSL); // parse percentiles percentiles := qantilesSL[0].Split([';']); if k <= qantilesSL.Count - 1 then begin // parse chiSquareTable chiSquareValuesTableArray := qantilesSL[k].Split([';']); for i := High(chiSquareValuesTableArray) downto Low(chiSquareValuesTableArray) do // trying get appropriate percentile begin if chiSquare < chiSquareValuesTableArray[i].ToDouble() then begin result := true; percentile := percentiles[i].ToDouble(); // percentile at which distribution is normal! chiSquareTable := chiSquareValuesTableArray[i].ToDouble(); Exit; end; end; end; finally qantilesSL.Free(); end; except result := false; chiSquareTable := -1; // default values chiSquare := -1; percentile := -1; end; end; class function TMyMath.isDistributionNormalSearchMaxPercentile(AValues: TArray<double>; var aFreedomCount: integer; var percentile, chiSquare, chiSquareTable: extended): Boolean; var resultPercentileSL: TStringList; resultFreeDomCountSL: TStringList; resultChiSquareSL: TStringList; resultChiSquareTableSL: TStringList; i: integer; // intervals; maxPercentile: extended; maxIndex: integer; resultIsNormalSL: TStringList; r: Boolean; begin result := false; //Tarray.Sort<double>(AValues); // sort first resultPercentileSL := TStringList.Create; resultFreeDomCountSL := TStringList.Create; resultChiSquareSL := TStringList.Create; resultChiSquareTableSL := TStringList.Create; resultIsNormalSL := TStringList.Create; try // https://ru.wikipedia.org/wiki/%D0%9A%D0%B2%D0%B0%D0%BD%D1%82%D0%B8%D0%BB%D0%B8_%D1%80%D0%B0%D1%81%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F_%D1%85%D0%B8-%D0%BA%D0%B2%D0%B0%D0%B4%D1%80%D0%B0%D1%82 for i := 2 to 50 do begin r := isDistributionNormal(AValues, i, aFreedomCount, percentile, chiSquare, chiSquareTable); if r then resultIsNormalSL.Add('1') else resultIsNormalSL.Add('0'); resultFreeDomCountSL.Add(aFreedomCount.ToString()); resultPercentileSL.Add(percentile.ToString()); resultChiSquareSL.Add(chiSquare.ToString()); resultChiSquareTableSL.Add(chiSquareTable.ToString()); end; // search max percentile // initial value maxPercentile := resultPercentileSL[3].ToDouble; maxIndex := -1; //max value if resultPercentileSL.Count > 0 then begin //maxPercentile := resultPercentileSL[0].ToDouble; for i := 3 to resultPercentileSL.Count - 1 do begin if (resultPercentileSL[i].ToDouble > maxPercentile) and (i > 3) then begin maxPercentile := resultPercentileSL[i].ToDouble; maxIndex := i; end; end; if maxIndex = -1 then maxIndex := 3; // writing answer aFreedomCount := resultFreeDomCountSL[maxIndex].ToInteger; percentile := resultPercentileSL[maxIndex].ToDouble; chiSquare := resultChiSquareSL[maxIndex].ToDouble; chiSquareTable := resultChiSquareTableSL[maxIndex].ToDouble; if resultIsNormalSL[maxIndex] = '1' then result := true else result := false; end; finally resultPercentileSL.Free(); resultFreeDomCountSL.Free(); resultChiSquareSL.Free(); resultChiSquareTableSL.Free(); resultIsNormalSL.Free(); end; end; |
additional functions
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
class function TMyMath.Simpson(Fun: TFunction; a, b, eps: double): double; // count definitive integral var i, n: integer; h, s0, s: double; begin n := 1; s := 0; repeat n := n * 2; h := (b - a) / n; s0 := s; s := Fun(a) + Fun(b); for i := 1 to n - 1 do s := s + 2 * (1 + i mod 2) * Fun(a + i * h); s := s * (b - a) / (3 * n); until abs(s - s0) <= eps; result := s; end; class procedure TMyMath.TestisDistributionNormal; var chiSquare: Double; mx, sDev: double; values: TArray<double>; chi: double; i: Integer; percentile: double; begin // create random values for i := 0 to 400 do begin SetLength(values, Length(values) + 1); values[High(values)] := RandG(130, 50); // Random(1000); // << never normal distr end; // count chiSquare isDistributionNormal(values, percentile); end; //Simpson // under Integral expression for counting of Laplas function class function TMyMath.Fun(t: double): double; begin result := exp(-t * t / 2); end; //Fun // normalized Laplas function class function TMyMath.Laplas(x: double): double; begin result := Simpson(Fun, 0, x, 1E-12) / sqrt(2 * pi); end; //F |
table of quantiles from wicki
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 |
class procedure TMyMath.createFQuantiles(var aQuantiles: TStringList); var i, j: Integer; splittedArray: array of string; begin for i := 0 to 50 do aQuantiles.Add(' '); // https://ru.wikipedia.org/wiki/%D0%9A%D0%B2%D0%B0%D0%BD%D1%82%D0%B8%D0%BB%D0%B8_%D1%80%D0%B0%D1%81%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F_%D1%85%D0%B8-%D0%BA%D0%B2%D0%B0%D0%B4%D1%80%D0%B0%D1%82 aQuantiles[0] := '0,01;0,025;0,05;0,1;0,2;0,3;0,4;0,5;0,6;0,7;0,8;0,9;0,95;0,975;0,99'; // quantiles aQuantiles[1] := '6,6349;5,0239;3,8415;2,7055;1,6424;1,0742;0,7083;0,4549;0,275;0,1485;0,0642;0,0158;0,0039;0,001;0,0002'; aQuantiles[2] := '9,2103;7,3778;5,9915;4,6052;3,2189;2,4079;1,8326;1,3863;1,0217;0,7133;0,4463;0,2107;0,1026;0,0506;0,0201'; aQuantiles[3] := '11,345;9,3484;7,8147;6,2514;4,6416;3,6649;2,9462;2,366;1,8692;1,4237;1,0052;0,5844;0,3518;0,2158;0,1148'; aQuantiles[4] := '13,277;11,143;9,4877;7,7794;5,9886;4,8784;4,0446;3,3567;2,7528;2,1947;1,6488;1,0636;0,7107;0,4844;0,2971'; aQuantiles[5] := '15,086;12,833;11,07;9,2364;7,2893;6,0644;5,1319;4,3515;3,6555;2,9999;2,3425;1,6103;1,1455;0,8312;0,5543'; aQuantiles[6] := '16,812;14,449;12,592;10,645;8,5581;7,2311;6,2108;5,3481;4,5702;3,8276;3,0701;2,2041;1,6354;1,2373;0,8721'; aQuantiles[7] := '18,475;16,013;14,067;12,017;9,8032;8,3834;7,2832;6,3458;5,4932;4,6713;3,8223;2,8331;2,1673;1,6899;1,239'; aQuantiles[8] := '20,09;17,535;15,507;13,362;11,03;9,5245;8,3505;7,3441;6,4226;5,5274;4,5936;3,4895;2,7326;2,1797;1,6465'; aQuantiles[9] := '21,666;19,023;16,919;14,684;12,242;10,656;9,4136;8,3428;7,357;6,3933;5,3801;4,1682;3,3251;2,7004;2,0879'; aQuantiles[10] := '23,209;20,483;18,307;15,987;13,442;11,781;10,473;9,3418;8,2955;7,2672;6,1791;4,8652;3,9403;3,247;2,5582'; aQuantiles[11] := '24,725;21,92;19,675;17,275;14,631;12,899;11,53;10,341;9,2373;8,1479;6,9887;5,5778;4,5748;3,8157;3,0535'; aQuantiles[12] := '26,217;23,337;21,026;18,549;15,812;14,011;12,584;11,34;10,182;9,0343;7,8073;6,3038;5,226;4,4038;3,5706'; aQuantiles[13] := '27,688;24,736;22,362;19,812;16,985;15,119;13,636;12,34;11,129;9,9257;8,6339;7,0415;5,8919;5,0088;4,1069'; aQuantiles[14] := '29,141;26,119;23,685;21,064;18,151;16,222;14,685;13,339;12,078;10,821;9,4673;7,7895;6,5706;5,6287;4,6604'; aQuantiles[15] := '30,578;27,488;24,996;22,307;19,311;17,322;15,733;14,339;13,03;11,721;10,307;8,5468;7,2609;6,2621;5,2293'; aQuantiles[16] := '32;28,845;26,296;23,542;20,465;18,418;16,78;15,338;13,983;12,624;11,152;9,3122;7,9616;6,9077;5,8122'; aQuantiles[17] := '33,409;30,191;27,587;24,769;21,615;19,511;17,824;16,338;14,937;13,531;12,002;10,085;8,6718;7,5642;6,4078'; aQuantiles[18] := '34,805;31,526;28,869;25,989;22,76;20,601;18,868;17,338;15,893;14,44;12,857;10,865;9,3905;8,2307;7,0149'; aQuantiles[19] := '36,191;32,852;30,144;27,204;23,9;21,689;19,91;18,338;16,85;15,352;13,716;11,651;10,117;8,9065;7,6327'; aQuantiles[20] := '37,566;34,17;31,41;28,412;25,038;22,775;20,951;19,337;17,809;16,266;14,578;12,443;10,851;9,5908;8,2604'; aQuantiles[21] := '38,932;35,479;32,671;29,615;26,171;23,858;21,991;20,337;18,768;17,182;15,445;13,24;11,591;10,283;8,8972'; aQuantiles[22] := '40,289;36,781;33,924;30,813;27,301;24,939;23,031;21,337;19,729;18,101;16,314;14,041;12,338;10,982;9,5425'; aQuantiles[23] := '41,638;38,076;35,172;32,007;28,429;26,018;24,069;22,337;20,69;19,021;17,187;14,848;13,091;11,689;10,196'; aQuantiles[24] := '42,98;39,364;36,415;33,196;29,553;27,096;25,106;23,337;21,652;19,943;18,062;15,659;13,848;12,401;10,856'; aQuantiles[25] := '44,314;40,646;37,652;34,382;30,675;28,172;26,143;24,337;22,616;20,867;18,94;16,473;14,611;13,12;11,524'; aQuantiles[26] := '45,642;41,923;38,885;35,563;31,795;29,246;27,179;25,336;23,579;21,792;19,82;17,292;15,379;13,844;12,198'; aQuantiles[27] := '46,963;43,195;40,113;36,741;32,912;30,319;28,214;26,336;24,544;22,719;20,703;18,114;16,151;14,573;12,879'; aQuantiles[28] := '48,278;44,461;41,337;37,916;34,027;31,391;29,249;27,336;25,509;23,647;21,588;18,939;16,928;15,308;13,565'; aQuantiles[29] := '49,588;45,722;42,557;39,087;35,139;32,461;30,283;28,336;26,475;24,577;22,475;19,768;17,708;16,047;14,256'; aQuantiles[30] := '50,892;46,979;43,773;40,256;36,25;33,53;31,316;29,336;27,442;25,508;23,364;20,599;18,493;16,791;14,953'; aQuantiles[31] := '52,191;48,232;44,985;41,422;37,359;34,598;32,349;30,336;28,409;26,44;24,255;21,434;19,281;17,539;15,655'; aQuantiles[32] := '53,486;49,48;46,194;42,585;38,466;35,665;33,381;31,336;29,376;27,373;25,148;22,271;20,072;18,291;16,362'; aQuantiles[33] := '54,776;50,725;47,4;43,745;39,572;36,731;34,413;32,336;30,344;28,307;26,042;23,11;20,867;19,047;17,074'; aQuantiles[34] := '56,061;51,966;48,602;44,903;40,676;37,795;35,444;33,336;31,313;29,242;26,938;23,952;21,664;19,806;17,789'; aQuantiles[35] := '57,342;53,203;49,802;46,059;41,778;38,859;36,475;34,336;32,282;30,178;27,836;24,797;22,465;20,569;18,509'; aQuantiles[36] := '58,619;54,437;50,998;47,212;42,879;39,922;37,505;35,336;33,252;31,115;28,735;25,643;23,269;21,336;19,233'; aQuantiles[37] := '59,893;55,668;52,192;48,363;43,978;40,984;38,535;36,336;34,222;32,053;29,635;26,492;24,075;22,106;19,96'; aQuantiles[38] := '61,162;56,896;53,384;49,513;45,076;42,045;39,564;37,335;35,192;32,992;30,537;27,343;24,884;22,878;20,691'; aQuantiles[39] := '62,428;58,12;54,572;50,66;46,173;43,105;40,593;38,335;36,163;33,932;31,441;28,196;25,695;23,654;21,426'; aQuantiles[40] := '63,691;59,342;55,758;51,805;47,269;44,165;41,622;39,335;37,134;34,872;32,345;29,051;26,509;24,433;22,164'; aQuantiles[41] := '64,95;60,561;56,942;52,949;48,363;45,224;42,651;40,335;38,105;35,813;33,251;29,907;27,326;25,215;22,906'; aQuantiles[42] := '66,206;61,777;58,124;54,09;49,456;46,282;43,679;41,335;39,077;36,755;34,157;30,765;28,144;25,999;23,65'; aQuantiles[43] := '67,459;62,99;59,304;55,23;50,548;47,339;44,706;42,335;40,05;37,698;35,065;31,625;28,965;26,785;24,398'; aQuantiles[44] := '68,71;64,201;60,481;56,369;51,639;48,396;45,734;43,335;41,022;38,641;35,974;32,487;29,787;27,575;25,148'; aQuantiles[45] := '69,957;65,41;61,656;57,505;52,729;49,452;46,761;44,335;41,995;39,585;36,884;33,35;30,612;28,366;25,901'; aQuantiles[46] := '71,201;66,617;62,83;58,641;53,818;50,507;47,787;45,335;42,968;40,529;37,795;34,215;31,439;29,16;26,657'; aQuantiles[47] := '72,443;67,821;64,001;59,774;54,906;51,562;48,814;46,335;43,942;41,474;38,708;35,081;32,268;29,956;27,416'; aQuantiles[48] := '73,683;69,023;65,171;60,907;55,993;52,616;49,84;47,335;44,915;42,42;39,621;35,949;33,098;30,755;28,177'; aQuantiles[49] := '74,919;70,222;66,339;62,038;57,079;53,67;50,866;48,335;45,889;43,366;40,534;36,818;33,93;31,555;28,941'; aQuantiles[50] := '76,154;71,42;67,505;63,167;58,164;54,723;51,892;49,335;46,864;44,313;41,449;37,689;34,764;32,357;29,707'; end; |




