Своими словами.
Обходятся все вершины. Для каждой вершины выбираются инцидентные ребра.
Просматриваются противоположные вершины инцидентных ребер и добавляются в очередь.
Просматривается очередь и выбирается ребро с наименьшим весом. Оно добавляется в финальную очередь.
Также должна быть проверка на то, что дерево это дерево, то есть Ациклический граф, поэтому если в нашем дереве есть 2 вершины, соединенные ребром, то такие ребра надо исключать.
Но есть 2 реализации алгоритма Прима – ленивая (ребра, образующие циклы не исключаются сразу) и энергичная (ребра, образующие циклы, исключаются сразу)
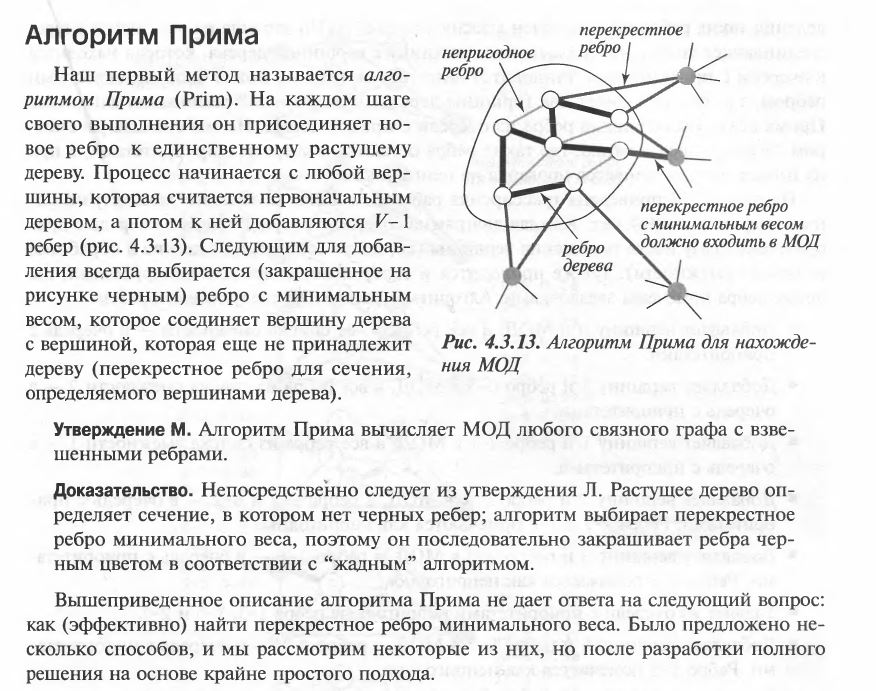
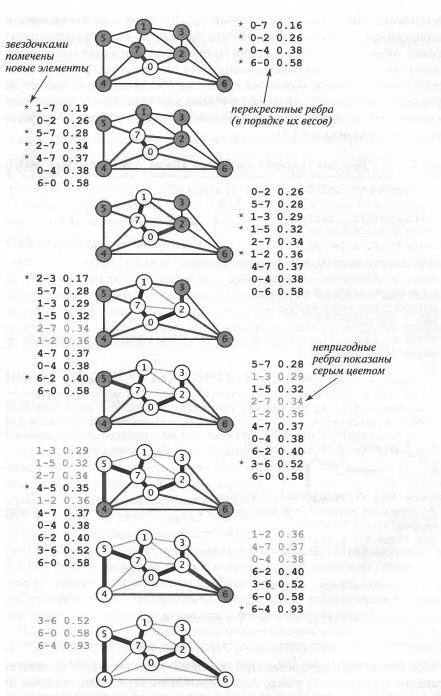
Теперь немного теории из Сэйджвика
Теперь немного кода на C#
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 |
using System; using System.Collections.Generic; using System.Diagnostics; using System.Linq; using System.Text; using System.Threading.Tasks; namespace WGraph { class LazyPrimMST // getting minimum spanning tree or mininmum spanning forest in edge weighted graph { private double FLOATING_POINT_EPSILON = 1E-12; private double weight; // total weight of MST private Queue<Edge> mst; // edges in mst private bool[] marked; private MinPQ<Edge> pq; public LazyPrimMST(EdgeWeightedGraph G) { mst = new Queue<Edge>(); marked = new bool[G.GetVertices()]; Comparer<Edge> comparer = Comparer<Edge>.Default; pq = new MinPQ<Edge>(1, comparer); for (int v = 0; v < G.GetVertices(); v++) { // to do if (!marked[v]) Prim(G, v); } } private void Prim(EdgeWeightedGraph G, int s) { Scan(G, s); while (!pq.IsEmpty()) { Edge e = pq.DelMin(); int v = e.Either(); int w = e.Other(v); Debug.Assert(marked[v] || marked[w]); if (marked[v] && marked[w]) continue; mst.Enqueue(e); weight += e.GetWeight(); if (!marked[v]) Scan(G, v); if (!marked[v]) Scan(G, v); } } private void Scan(EdgeWeightedGraph G, int v) { Debug.Assert(!marked[v]); marked[v] = true; foreach (Edge e in G.GetAdj(v)) { if (!marked[e.Other(v)]) pq.Insert(e); } } public IEnumerable<Edge> GetEdges() { return mst; } public double GetWeight() { return weight; } } } |
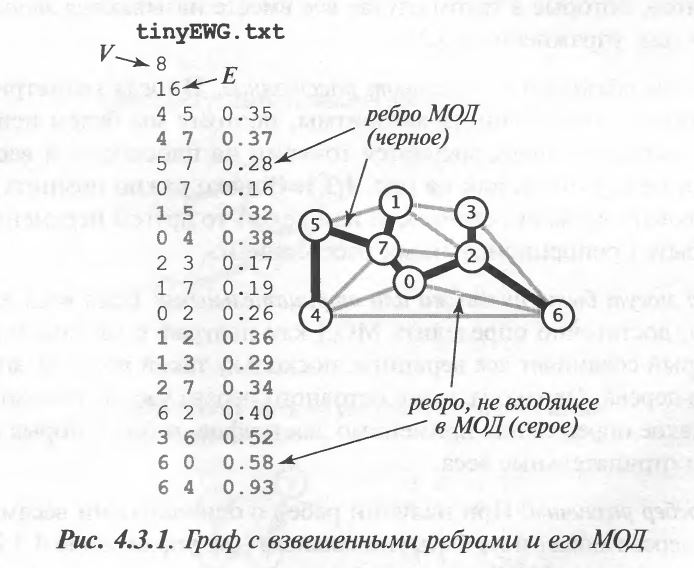
Попробуем этот алгоритм на таком графе
Вот тестовый клиент
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
Console.WriteLine(" "); Console.WriteLine("LazyPrimMST "); LazyPrimMST lazyPrimMST = new LazyPrimMST(G); Queue<Edge> minSpanningTreeQueue = new Queue<Edge>(); minSpanningTreeQueue= (Queue<Edge>)(lazyPrimMST.GetEdges()); Console.WriteLine("weight of minimal spanning tree tree is " + lazyPrimMST.GetWeight()); foreach (Edge e in minSpanningTreeQueue) { int v = e.Either(); int w = e.Other(v); Console.WriteLine(v +" - " + w); } |
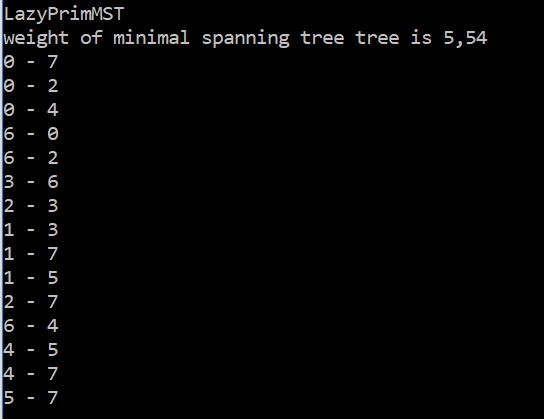
А вот и результат
Здесь есть ребра, которые соединяют 2 вершины дерева, и у нас получается цикл. Но в ленивом варианте алгоритма Прима мы на этом останавливаемся. Если использовать этот вариант, то для получения минимального остовного дерева нам нужно удалить ребра, которые соединяют 2 вершины дерева отдельным алгоритмом, чтобы исключить циклы. В энергичном же варианте алгоритма Прима, будем удалять ребра по ходу алгоритма.