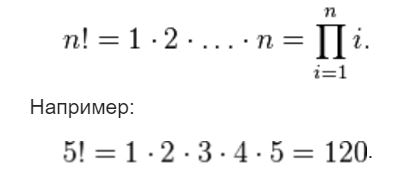Данная статья посвящена рекурсии. Понравились картинки из сети на тему рекурсии)))
Элементарно, ребята!
Если по простому, то рекурсия функции / процедуры – это вызов самой себя, в своём же теле. Например так…
|
1 2 3 4 |
procedure SomeProcedure; begin SomeProcedure; end; |
Но если нет цели – подвесить систему – лучше так не делать. Процедура вызывает саму себя бесконечно и ничего не происходит, кроме этого, отсутствует так называемая терминальная ветвь рекурсии. Даже если убрать это “удовольствие” в отдельный поток – ресурсы системы будут расходоваться. Нужен какой-то выход из рекурсии. Самое простое – дописать счетчик, например так…
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
var Count:integer; // Глобальная переменная - счетчик вызовов процедуры ... procedure SomeProcedure(N:Integer); // N - счетчик терминальной ветви рекурсии begin if N=0 then exit; // Вот она - терминальная ветвь рекурсии! Dec(N); // Уменьшаем N, чтобы выйти из рекурсии Inc(Count); // Считаем сколько раз вызвали процедуру SomeProcedure(N); end; ... |
В Википедии очень хорошо и подробно написано на эту тему. Цитирую
Структурно рекурсивная функция / процедура на верхнем уровне всегда представляет собой команду ветвления (выбор одной из двух или более альтернатив в зависимости от условия (условий), которое в данном случае уместно назвать «условием прекращения рекурсии»), имеющей две или более альтернативные ветви, из которых хотя бы одна является рекурсивной и хотя бы одна — терминальной. Рекурсивная ветвь выполняется, когда условие прекращения рекурсии ложно, и содержит хотя бы один рекурсивный вызов — прямой или опосредованный вызов функцией самой себя. Терминальная ветвь выполняется, когда условие прекращения рекурсии истинно;
От себя что хочу сказать. В том виде, в котором рекурсия показана выше – она практически бессмысленна, разве что для теории – понять, что это такое. А суть в чем, в жизни встречаются такие задачи, которые можно решать рекурсивно. Просто люди как правило привыкли мыслить линейно может потому что время линейно.
Красим забор рекурсивно!
В одной из книг по алгоритмам, прочитал про покраску забора – можно покрасить его слева направо как единое целое, а можно разделить на 4 части и в определенной последовательности красить эти 4 части.
В псевдокоде это можно представить так
Процедура Покрасить забор (длина забора)
Начало
Если забор покрашен, то выйти из процедуры;
Процедура Покрасить забор (1 / 4 длины забора);
Перейти на следующую четверть;
Конец
Куда же без факториала?
Какой источник не возьми по рекурсиям – везде факториал ))). Не будем нарушать эту славную традицию 🙂
Но для начала вспомним что такое факториал, опять же из Википедии
Факториал это произведение всех натуральных чисел от 1 до n включительно:
Рекурсивная функция факториала в Delphi
|
1 2 3 4 5 6 7 |
Function Factorial (N:Longint):Longint; begin if N<=0 then Result:=1; // Терминальная ветвь рекурсии if N>0 then Result:=N*Factorial(N-1); end; |
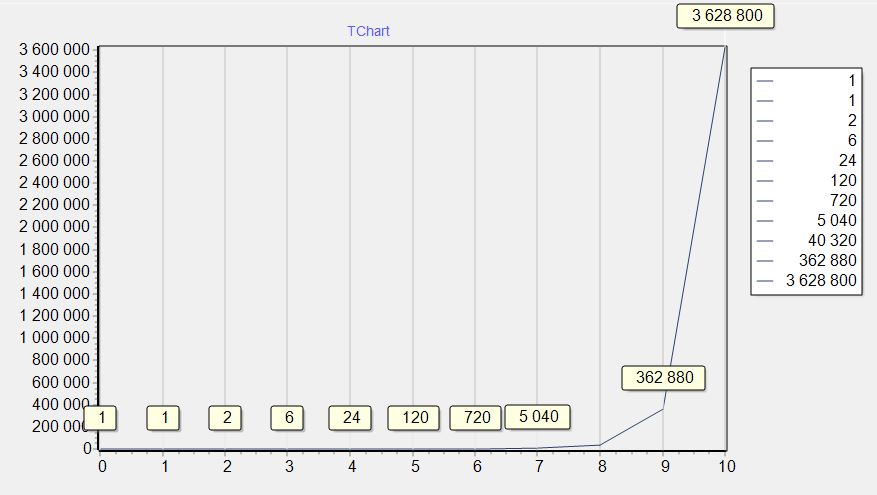
Сложность алгоритма оценивается как O(N). Эту функцию можно написать и не рекурсивно, но об этом в другой статье. Ради интереса посмотрим как ведет себя факториал
Движемся дальше.
Основа всего сущего – числа Фибоначи!
Рекурсивное определение чисел Фибоначи может быть таким
|
1 2 3 4 5 |
Fib(0)=0; Fib(1)=1; Fib(N)=Fib(N-1)+Fib(N-2) для N>1; |
Рекурсивная реализация на Delphi будет выглядеть таким образом
|
1 2 3 4 5 6 7 8 9 10 11 |
function Fibonachi (n:Longint):Longint; begin if n<0 then exit else // Проверка на положительность чисел if n<=1 then Result:=n // Терминальная ветвь рекурсии else Result:=Fibonachi(n-1)+Fibonachi(n-2); // Сама рекурсия end; |
Сложность алгоритма O(N);
Числа Фибоначи встречаются во многих уголках вселенной, например, ракушки…
Рекурсия и память
Известно, что когда мы используем процедуры и функции, то переменные внутри них “живут”, пока работает сама процедура или функция, но что происходит во время рекурсии? Когда мы N раз внутри одной процедуры открыли её саму же – ну логично! Все переменные N раз дублируются. Понимаете к чему я веду? Рекурсивные алгоритмы, не смотря на свою изящность – скажу по русски – “жрут” память. Что делать в таком случае? Варианта два. Первый – попробовать вынести локальные переменные в глобальные, и если это не помогло, то всё очень просто – заменить рекурсивный алгоритм на обычный.
Вот пример для факториала – переписали его в цикле, теперь память не “жрется”;
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
Function factorial(n:iteger):integer; begin Result:=1; while (n>1) do begin Result:=Result*(n); dec(n); end; //while end;// funciton |
Выводы по рекурсии
-Всегда писать терминальную ветвь
-При глубокой рекурсии – выносить переменные в глобальные, либо переписать алгоритм не рекурсивно.
Вообще говоря, на мой взгляд с рекурсией код изящней, но и сложнее для восприятия, да и для памяти – нагрузка. Как говорится – если можно лучше и проще, то давайте – лучше и проще!