Теория графов, университет ИТМО
Орграф – множество вершин и коллекция ориентированных ребер.
Полустепень исхода
Полустепень входа
Ориентированный путь орграфа – последовательность вершин, в которой существует ориентированное ребро, указывающее из каждой вершины на след. вершину этой последовательности.
Ориентированный цикл – ориентированный путь, содержащий как минимум 1 ребро, в котором 1 и последняя вершины совпадают.
Длина пути цикла – количество ребер в нем.
Простой цикл – без повторяющихся ребер и вершин (кроме обязательного совпадения 1 и последней вершины)
Достижимость из v в w, если существует ориентированный путь из v в w.
Представление ориентированного графа в файле
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
13 22 4 2 2 3 3 2 6 0 0 1 2 0 11 12 12 9 9 10 9 11 8 9 10 12 11 4 4 3 3 5 7 8 8 7 5 4 0 5 6 4 6 9 7 6 |
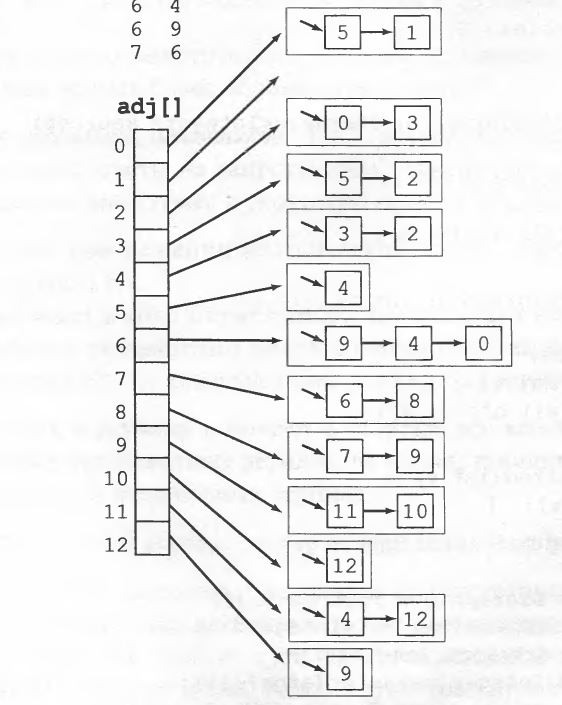
Представление орграфа списками смежности
Разница в представлении с неориентированными графами. Для неориентированных графов, если v находится в списке смежности вершины w, то и w находится в списке смежности вершины v. Однако, в представлении списками смежности для орграфов такой симметрии нет. Каждое ребро присутствует в списке смежности только один раз.
Достижимость и связность
Можно легко сказать связаны ли вершины v и w, но сложно сказать, можно ли достичь вершины w из v.