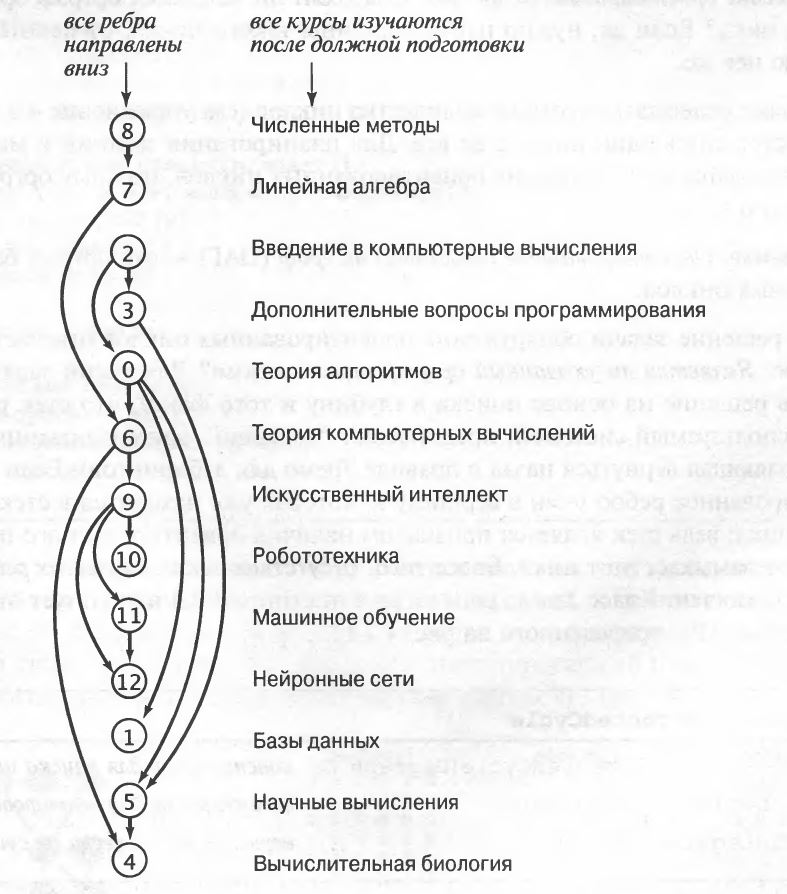
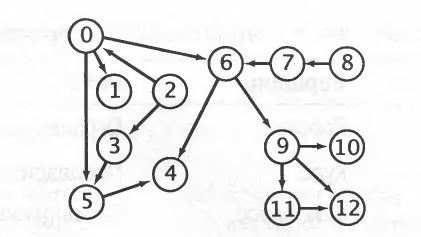
Граф тестирования…
Представление в текстовом файле
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
13 14 0 5 0 6 0 1 2 0 2 3 3 5 5 4 6 4 7 6 8 7 9 10 9 11 9 12 11 12 |
Клиент тестирования будет выглядеть так…
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
G = new Digraph("tinyDG_noCycles.txt"); // <<< setting new Graph Console.WriteLine(" --- Topological reversePostOrder, changing to tinyDG_noCycles.txt"); isCycle = G.IsCycle(G); if (!isCycle) { Stack<int> TopologicalOrder = G.GetTopologicalOrder(G); while (TopologicalOrder.Count != 0) { Console.WriteLine(TopologicalOrder.Pop()); } } else { if (isCycle) Console.WriteLine("Topological order impossible, there is cycle there... "); } |
Допишем класс Digraph
|
1 2 3 4 5 6 |
// --- Topological Order... public Stack<int> GetTopologicalOrder(Digraph G) { DigraphTopological2 o = new DigraphTopological2(G); return new Stack<int>(o.Order); } |
 Класс топологической сортировки
Класс топологической сортировки
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 |
using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; namespace Digraph { class DigraphTopological2 /* topological order of graph without cycles, if cycles - no topological order */ { public IEnumerable<int> Order { get; set; } // topological order private int[] rank; // rank of vertex v in order private int V; /** * Determines whether the digraph {@code G} has a topological order and, if so, * finds such a topological order. * @param G the digraph */ public DigraphTopological2(Digraph G) { V = G.GetVertices(); DirectedCycle finder = new DirectedCycle(G); if (!finder.IsCycle()) { DigraphTopological d = new DigraphTopological(G); Order = d.ReversePost; rank = new int[G.GetVertices()]; int i = 0; foreach (int v in Order) { rank[v] = i++; } } } // --- public bool IsOrder() { return Order != null; } // --- public int GetRank(int v) { ValidateVertex(v); if (Order != null) return rank[v]; else return -1; } // --- Validation... private void ValidateVertex(int v) { if (v < 0 || v >= V) { throw new ArgumentException("vertex " + v + " is not between 0 and " + "(V - 1)"); } } } } |
Вспомогательный класс для определения порядков обхода вершин графа
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; namespace Digraph { class DigraphTopological { private Boolean[] marked; // marked[v] = true if v is reachable from source(s) public Queue<int> Pre { get; } public Queue<int> Post { get; } public Stack<int> ReversePost { get; } public DigraphTopological(Digraph G) { Pre = new Queue<int>(); Post = new Queue<int>(); ReversePost = new Stack<int>(); marked = new bool[G.GetVertices()]; for (int v=0; v < G.GetVertices(); v++) if (!marked[v]) Dfs(G, v); } private void Dfs(Digraph G, int v) { marked[v] = true; Pre.Enqueue(v); foreach (int w in G.GetAdj(v)) { if (!marked[w]) Dfs(G, w); } Post.Enqueue(v); ReversePost.Push(v); } // --- validation private void ValidateVertex(int v) { int V = marked.Length; if (v < 0 || v >= V) { throw new ArgumentException("vertex " + v + " is not between 0 and " + "(V - 1)"); } } } } |