Сложность алгоритма Косараю V+E
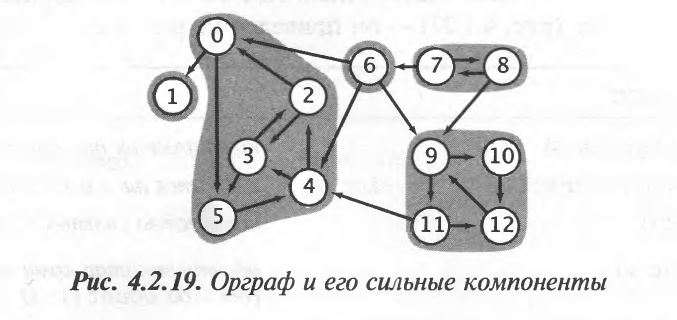
Рассмотрим граф
Серым цветом отмечены области сильно связных компонентов.
Клиент тестирования будет выглядеть следующим образом. Из графа выше видно, что 0 и 2 это сильно связные компоненты, а 0 и 1 нет.
|
1 2 3 4 5 |
// -- Kosaraju, strongly connected components Console.WriteLine("Kosaraju IsStronglyConnected 0 and 2 "); Console.WriteLine(G.IsStronglyConnected(G,0,2)); Console.WriteLine("Kosaraju IsStronglyConnected 0 and 1 "); Console.WriteLine(G.IsStronglyConnected(G, 0, 1)); |
Клиент тестирования полностью
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 |
using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; namespace Digraph { class Program { static void Main(string[] args) { Digraph G = new Digraph("tinyDG.txt"); //how much vertices? Console.WriteLine("Vertices: " + G.GetVertices()); //how much edges? Console.WriteLine("Edges: " + G.GetEdges()); // indegree Console.WriteLine("InDegree for 0 vertice: " + G.GetInDegree(0)); // outdegree Console.WriteLine("OutDegree for 0 vertice: " + G.GetOutDegree(0)); // is v reachible from s ? Console.WriteLine("is 1 reachible from 0: " + G.IsReachible(G, 0, 1)); // True Console.WriteLine("is 6 reachible from 0: " + G.IsReachible(G, 0, 1)); // False int s = 0; // start vertex int f = 2; // finish vertex // --- DFS Console.WriteLine(" --- DFS..."); // Has path to ? Console.WriteLine("Has path from " + s + " to " + f + " vertex, DFS? " + G.IsPathToDFS(G, s, f)); // This is the path, DFS Console.WriteLine("This is the path, DFS?"); Stack<int> path = new Stack<int>(); G.GetPathToDFS(G, s, f, ref path); if (path.Count != 0) { foreach (int i in path) Console.WriteLine(" > " + i.ToString()); } else Console.WriteLine("no path..."); // --- BFS Console.WriteLine("--- BFS..."); // Haspath to Console.WriteLine("Has path from " + s + " to " + f + " vertex, DFS? " + G.IsPathToBFS(G, s, f)); // --- shortest distance path.Clear(); if (G.IsPathToBFS(G, s, f)) Console.WriteLine("Shortest distance: " + G.GetShortestDistToBFS(G, s, f)); // --- Console.WriteLine("This is the path, DFS?"); G.GetShortestPathToBFS(G, s, f, ref path); if (path.Count != 0) { foreach (int i in path) Console.WriteLine(" > " + i.ToString()); } else Console.WriteLine("no path..."); //--- Cycles bool isCycle = G.IsCycle(G); Console.WriteLine("Is Cycle? " + isCycle); if (isCycle) { Stack<int> cycle = new Stack<int>(); cycle = G.GetCycle(G); foreach (int v in cycle) Console.WriteLine(v); } // -- Kosaraju, strongly connected components Console.WriteLine("Kosaraju IsStronglyConnected 0 and 2 "); Console.WriteLine(G.IsStronglyConnected(G,0,2)); Console.WriteLine("Kosaraju IsStronglyConnected 0 and 1 "); Console.WriteLine(G.IsStronglyConnected(G, 0, 1)); // --- Topological Queue<int> preOrder = G.GetPreOrder(G); Console.WriteLine(" ---preOrder"); while (preOrder.Count != 0) { Console.WriteLine(preOrder.Dequeue()); } Queue<int> postOrder = G.GetPostOrder(G); Console.WriteLine(" ---postOrder"); while (postOrder.Count != 0) { Console.WriteLine(postOrder.Dequeue()); } /* Stack<int> reversePost = G.GetReversePostOrder(G); Console.WriteLine(" ---reversePostOrder"); while (reversePost.Count != 0) { Console.WriteLine(reversePost.Pop()); } */ // G = new Digraph("tinyDG_noCycles.txt"); // <<< setting new Graph Console.WriteLine(" --- Topological reversePostOrder, changing to tinyDG_noCycles.txt"); isCycle = G.IsCycle(G); if (!isCycle) { Stack<int> TopologicalOrder = G.GetTopologicalOrder(G); while (TopologicalOrder.Count != 0) { Console.WriteLine(TopologicalOrder.Pop()); } } else { if (isCycle) Console.WriteLine("Topological order impossible, there is cycle there... "); } // --- just describing the orGraph... toString() Console.WriteLine(); Console.WriteLine("---ToString(): " + G.ToString()); Console.ReadLine(); } } } |
Класс Kosaraju, который даст нам возможность определять сильную связность компонентов
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 |
using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; namespace Digraph { class KosarajuSCC // Kosaraju Strong Connected Components { private bool[] marked; private int[] id; private int count; // public KosarajuSCC(Digraph G) { marked = new bool[G.GetVertices()]; id = new int[G.GetVertices()]; DigraphTopological d = new DigraphTopological(G.Reverse()); foreach (int s in d.ReversePost) // reversePost Order here { if (!marked[s]) { Dfs(G, s); count++; } } } // DFS on graph G private void Dfs(Digraph G, int v) { marked[v] = true; id[v] = count; foreach (int w in G.GetAdj(v)) { if (!marked[w]) Dfs(G, w); } } public bool IsStronglyConnected(int v, int w) { return id[v] == id[w]; } public int GetID(int v) { return id[v]; } public int GetCount() { return count; } } } |