В данном разделе рассмотрим теорию из Сейджвика про очередь с приоритетами и бинарную пирамиду. Последнюю используем в качестве структуры данных для реализации очереди с приоритетами.
В данном случае напишем очередь, которая поддерживает
- вставку элемента
- получение элемента с максимальным ключом
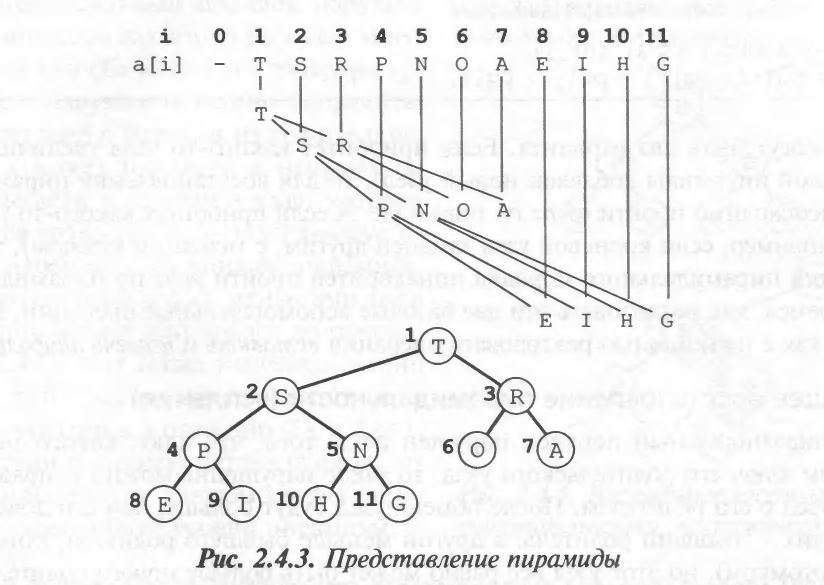
Идея алгоритма в том, что в качестве бинарной пирамиды мы будем использовать массив. В этот массив мы будем вставлять данные и получать их из него. При каждой вставке, получении, целостность пирамиды у нас будет возможно нарушаться, поэтому мы будем частично обходить пирамиду для восстановления целостности. Такой обход будет стоить логарифмического времени. Что позволит работать с огромными данными.
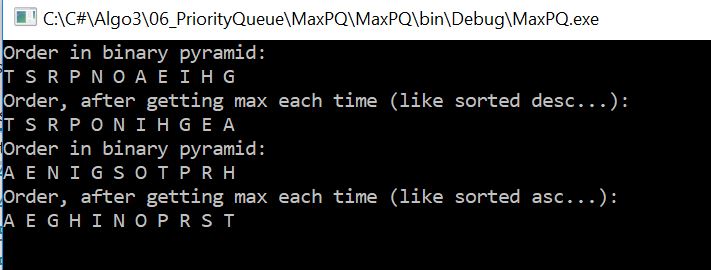
По сути, если пройтись циклом, доставая из контейнера все данные, мы получим отсортированные данные. В данном примере по убыванию. Но, нетрудно переписать алгоритм и для возрастающего случая, для этого надо доставать каждый раз из хранилища данные с минимальным ключом.


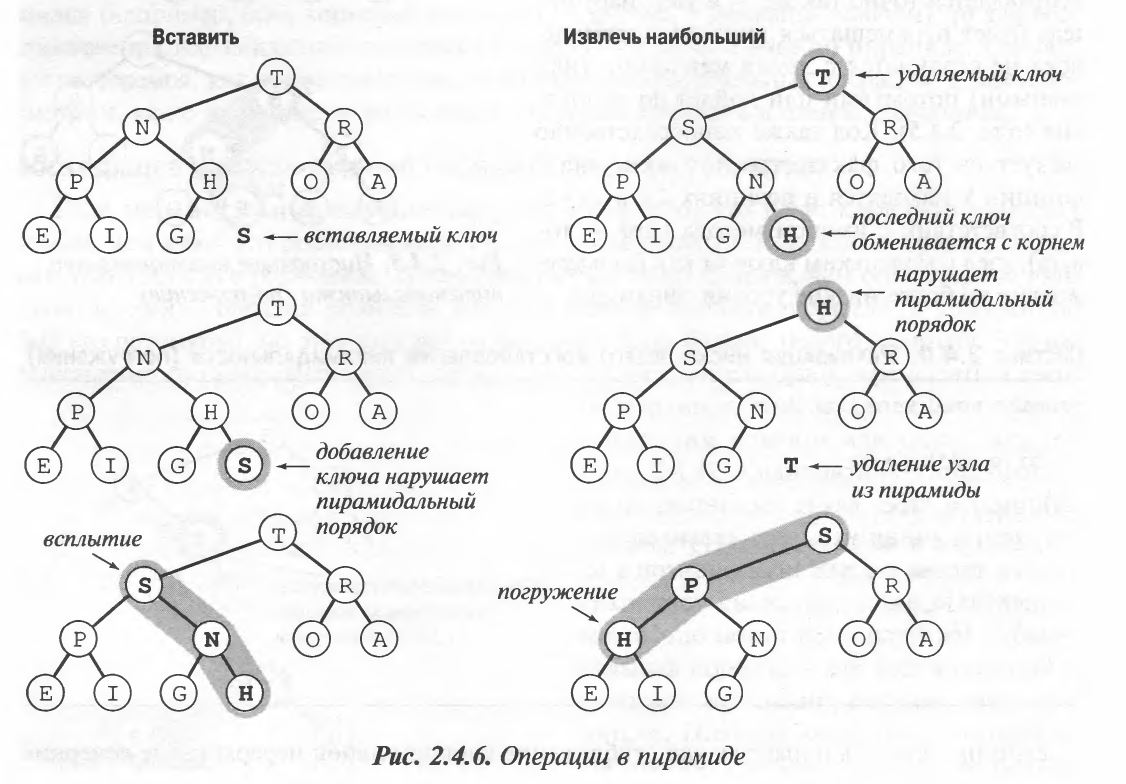
Используя эти знания, напишем класс очереди с приоритетами, используя в качестве структуры данных бинарную пирамиду. Основное его назначение – функции Insert и DelMax.
DelMax будет доставать максимальный элемент из очереди и удалять его из очереди.
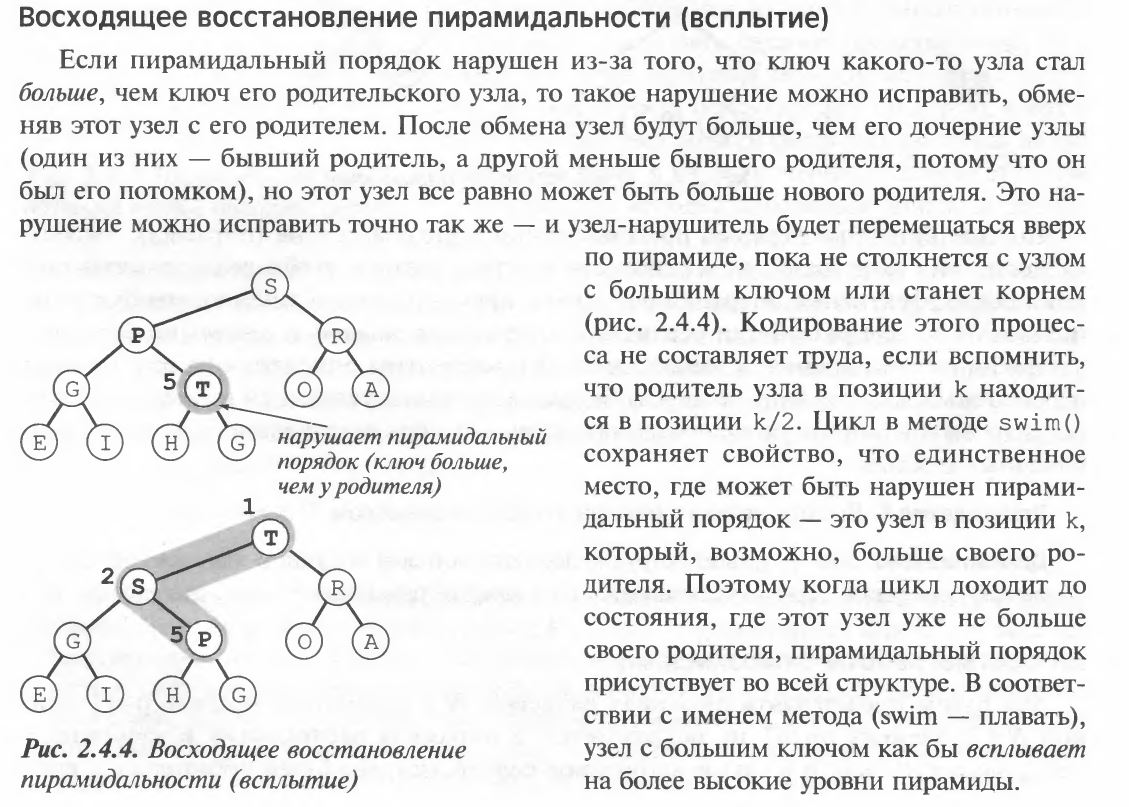
Как уже было сказано выше, основная идея в том, чтобы произвести некоторую операцию (вставку, получение максимального элемента) и восстановить пирамидальную целостность, частично обойдя пирамиду и переставляя элементы.
MaxPQ класс
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 |
using System; using System.Collections; using System.Collections.Generic; using System.Diagnostics; using System.Linq; using System.Text; using System.Threading.Tasks; namespace PriorityQueues { class MaxPQ<Key> :IEnumerable<Key> { private Key[] pq; // // store items at indices 1 to n, 0 not use.. private int n; // number of items on priority queue private Comparer<Key> comparer; // optional comparator // /** * Initializes an empty priority queue with the given initial capacity. * * @param initCapacity the initial capacity of this priority queue */ public MaxPQ(int initCapacity) { pq = new Key[initCapacity + 1]; n = 0; } /** * Initializes an empty priority queue with the given initial capacity, * using the given comparator. * * @param initCapacity the initial capacity of this priority queue * @param comparator the order in which to compare the keys */ public MaxPQ(int initCapacity, Comparer<Key> comparer) { this.comparer = comparer; pq = new Key[initCapacity + 1]; n = 0; } // --- one more init public MaxPQ(Comparer<Key> Comparer, int N, Key[] PQ) { this.comparer = Comparer; this.pq = PQ; this.n = N; } /** * Initializes an empty priority queue. */ public MaxPQ() { pq = new Key[1]; n = 0; } /** * Initializes an empty priority queue using the given comparator. * * @param comparator the order in which to compare the keys */ public MaxPQ(Comparer<Key> comparer) { this.comparer = comparer; pq = new Key[1]; n = 0; } /** * Adds a new key to this priority queue. * * @param x the new key to add to this priority queue */ public void Insert(Key x) { // double size of array if necessary if (n == pq.Length - 1) Resize(2 * pq.Length); // add x, and percolate it up to maintain heap invariant pq[++n] = x; Swim(n); Debug.Assert(IsMaxHeap()); } /** * Removes and returns a largest key on this priority queue. * * @return a largest key on this priority queue * @throws NoSuchElementException if this priority queue is empty */ public Key DelMax() { if (IsEmpty()) throw new ArgumentException("Priority queue underflow"); Key max = pq[1]; Exch(1, n--); Sink(1); pq[n + 1] = default(Key);// null; // to avoid loiterig and help with garbage collection if ((n > 0) && (n == (pq.Length - 1) / 4)) Resize(pq.Length / 2); Debug.Assert(IsMaxHeap()); return max; } /** * Returns true if this priority queue is empty. * * @return {@code true} if this priority queue is empty; * {@code false} otherwise */ public bool IsEmpty() { return n == 0; } // Returns the number of keys on this priority queue. public int Size() { return n; } // Returns a largest key on this priority queue. public Key Max() { if (IsEmpty()) throw new ArgumentException("Priority queue is empty"); return pq[1]; } // Helper function to double the size of the heap array private void Resize(int capacity) { Debug.Assert(capacity > n); Key[] temp = new Key[capacity]; for (int i = 1; i <= n; i++) { temp[i] = pq[i]; } pq = temp; } /*************************************************************************** * Helper functions to restore the heap invariant. ***************************************************************************/ private void Swim(int k) { while (k > 1 && Less(k / 2, k)) { Exch(k, k / 2); k = k / 2; } } private void Sink(int k) { while (2 * k <= n) { int j = 2 * k; if (j < n && Less(j, j + 1)) j++; if (!Less(k, j)) break; Exch(k, j); k = j; } } /*************************************************************************** * Helper functions for compares and swaps. ***************************************************************************/ private bool Less(int i, int j) { if (comparer == null) { //return Comparer<Key>(pq[i]).compareTo(pq[j]) < 0; throw new ArgumentException("comparer is null"); } else { return comparer.Compare(pq[i], pq[j]) < 0; } } private void Exch(int i, int j) { Key swap = pq[i]; pq[i] = pq[j]; pq[j] = swap; } // is pq[1..N] a max heap? private bool IsMaxHeap() { return IsMaxHeap(1); } // is subtree of pq[1..n] rooted at k a max heap? private bool IsMaxHeap(int k) { if (k > n) return true; int left = 2 * k; int right = 2 * k + 1; if (left <= n && Less(k, left)) return false; if (right <= n && Less(k, right)) return false; return IsMaxHeap(left) && IsMaxHeap(right); } // /* public IEnumerator<Key> Iterator() { return new HeapIterator<Key>(); } */ public IEnumerator<Key> GetEnumerator() { return new HeapIterator<Key>(comparer, Size(), n,pq); } IEnumerator IEnumerable.GetEnumerator() { return GetEnumerator(); } private class HeapIterator<Key> : IEnumerator<Key> { public Key[] PQ { get; set; } // // store items at indices 1 to n, 0 not use.. public int Size { get; set; } public int N { get; set; } public Comparer<Key> Comparer { get; set; } // private int position = -1; private MaxPQ<Key> copy; public HeapIterator() { if (Comparer == null) copy = new MaxPQ<Key>(Size); else copy = new MaxPQ<Key>(Size, Comparer); for (int i = 0; i < N; N++) copy.Insert(PQ[i]); } public HeapIterator(Comparer<Key> Comparer, int Size, int N, Key[] PQ) { this.Comparer = Comparer; this.Size = Size; this.N = N; this.PQ = PQ; if (Comparer == null) copy = new MaxPQ<Key>(Size); else copy = new MaxPQ<Key>(Size, Comparer); for (int i = 0; i <= N; i++) copy.Insert(this.PQ[i]); } public bool HasNext() { return !copy.IsEmpty(); } public void Remove() { throw new ArgumentException("error"); } public Key Next() { if (!HasNext()) throw new ArgumentException("error"); return copy.DelMax(); } public void Dispose() { //throw new NotImplementedException(); } public bool MoveNext() { position++; //return !copy.IsEmpty(); return position < copy.Size(); } public void Reset() { position = -1; } // object IEnumerator.Current { get { return Current; } } public Key Current { get { try { return PQ[position]; } catch (IndexOutOfRangeException) { throw new InvalidOperationException(); } } } } } } |
Аналогично MinPQ
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 |
using System; using System.Collections; using System.Collections.Generic; using System.Diagnostics; using System.Linq; using System.Text; using System.Threading.Tasks; namespace PriorityQueues { class MinPQ<Key> : IEnumerable<Key> { private Key[] pq; // // store items at indices 1 to n, 0 not use.. private int n; // number of items on priority queue private Comparer<Key> comparer; // optional comparator // /** * Initializes an empty priority queue with the given initial capacity. * * @param initCapacity the initial capacity of this priority queue */ public MinPQ(int initCapacity) { pq = new Key[initCapacity + 1]; n = 0; } /** * Initializes an empty priority queue with the given initial capacity, * using the given comparator. * * @param initCapacity the initial capacity of this priority queue * @param comparator the order in which to compare the keys */ public MinPQ(int initCapacity, Comparer<Key> comparer) { this.comparer = comparer; pq = new Key[initCapacity + 1]; n = 0; } // --- one more init public MinPQ(Comparer<Key> Comparer, int N, Key[] PQ) { this.comparer = Comparer; this.pq = PQ; this.n = N; } /** * Initializes an empty priority queue. */ public MinPQ() { pq = new Key[1]; n = 0; } /** * Initializes an empty priority queue using the given comparator. * * @param comparator the order in which to compare the keys */ public MinPQ(Comparer<Key> comparer) { this.comparer = comparer; pq = new Key[1]; n = 0; } /** * Adds a new key to this priority queue. * * @param x the new key to add to this priority queue */ public void Insert(Key x) { // double size of array if necessary if (n == pq.Length - 1) Resize(2 * pq.Length); // add x, and percolate it up to maintain heap invariant pq[++n] = x; Swim(n); Debug.Assert(IsMinHeap()); } /** * Removes and returns a largest key on this priority queue. * * @return a largest key on this priority queue * @throws NoSuchElementException if this priority queue is empty */ public Key DelMin() { if (IsEmpty()) throw new ArgumentException("Priority queue underflow"); Key min = pq[1]; Exch(1, n--); Sink(1); pq[n + 1] = default(Key);// null; // to avoid loiterig and help with garbage collection if ((n > 0) && (n == (pq.Length - 1) / 4)) Resize(pq.Length / 2); Debug.Assert(IsMinHeap()); return min; } /** * Returns true if this priority queue is empty. * * @return {@code true} if this priority queue is empty; * {@code false} otherwise */ public bool IsEmpty() { return n == 0; } // Returns the number of keys on this priority queue. public int Size() { return n; } // Returns a largest key on this priority queue. public Key Min() { if (IsEmpty()) throw new ArgumentException("Priority queue is empty"); return pq[1]; } // Helper function to double the size of the heap array private void Resize(int capacity) { Debug.Assert(capacity > n); Key[] temp = new Key[capacity]; for (int i = 1; i <= n; i++) { temp[i] = pq[i]; } pq = temp; } /*************************************************************************** * Helper functions to restore the heap invariant. ***************************************************************************/ private void Swim(int k) { while (k > 1 && Greater(k / 2, k)) { Exch(k, k / 2); k = k / 2; } } private void Sink(int k) { while (2 * k <= n) { int j = 2 * k; if (j < n && Greater(j, j + 1)) j++; if (!Greater(k, j)) break; Exch(k, j); k = j; } } /*************************************************************************** * Helper functions for compares and swaps. ***************************************************************************/ private bool Greater(int i, int j) { if (comparer == null) { //return Comparer<Key>(pq[i]).compareTo(pq[j]) < 0; throw new ArgumentException("comparer is null"); } else { return comparer.Compare(pq[i], pq[j]) > 0; } } private void Exch(int i, int j) { Key swap = pq[i]; pq[i] = pq[j]; pq[j] = swap; } // is pq[1..N] a max heap? private bool IsMinHeap() { return IsMinHeap(1); } // is subtree of pq[1..n] rooted at k a max heap? private bool IsMinHeap(int k) { if (k > n) return true; int left = 2 * k; int right = 2 * k + 1; if (left <= n && Greater(k, left)) return false; if (right <= n && Greater(k, right)) return false; return IsMinHeap(left) && IsMinHeap(right); } // /* public IEnumerator<Key> Iterator() { return new HeapIterator<Key>(); } */ public IEnumerator<Key> GetEnumerator() { return new HeapIterator<Key>(comparer, Size(), n, pq); } IEnumerator IEnumerable.GetEnumerator() { return GetEnumerator(); } private class HeapIterator<Key> : IEnumerator<Key> { public Key[] PQ { get; set; } // // store items at indices 1 to n, 0 not use.. public int Size { get; set; } public int N { get; set; } public Comparer<Key> Comparer { get; set; } // private int position = -1; private MaxPQ<Key> copy; public HeapIterator() { if (Comparer == null) copy = new MaxPQ<Key>(Size); else copy = new MaxPQ<Key>(Size, Comparer); for (int i = 0; i < N; N++) copy.Insert(PQ[i]); } public HeapIterator(Comparer<Key> Comparer, int Size, int N, Key[] PQ) { this.Comparer = Comparer; this.Size = Size; this.N = N; this.PQ = PQ; if (Comparer == null) copy = new MaxPQ<Key>(Size); else copy = new MaxPQ<Key>(Size, Comparer); for (int i = 0; i <= N; i++) copy.Insert(this.PQ[i]); } public bool HasNext() { return !copy.IsEmpty(); } public void Remove() { throw new ArgumentException("error"); } public Key Next() { if (!HasNext()) throw new ArgumentException("error"); return copy.DelMax(); } public void Dispose() { //throw new NotImplementedException(); } public bool MoveNext() { position++; //return !copy.IsEmpty(); return position < copy.Size(); } public void Reset() { position = -1; } // object IEnumerator.Current { get { return Current; } } public Key Current { get { try { return PQ[position]; } catch (IndexOutOfRangeException) { throw new InvalidOperationException(); } } } } } } |
Клиент тестирования будет выглядеть так…
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 |
using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; namespace PriorityQueues { class Program { static void Main(string[] args) { Comparer<string> comparer = Comparer<string>.Default; MaxPQ<string> maxPQ = new MaxPQ<string>(11, comparer); maxPQ.Insert("S"); maxPQ.Insert("T"); maxPQ.Insert("R"); maxPQ.Insert("P"); maxPQ.Insert("N"); maxPQ.Insert("O"); maxPQ.Insert("A"); maxPQ.Insert("E"); maxPQ.Insert("I"); maxPQ.Insert("H"); maxPQ.Insert("G"); Console.WriteLine("Order in binary pyramid: "); foreach (string s in maxPQ) { if(s!=null) Console.Write(s + " "); } Console.WriteLine(" "); Console.WriteLine("Order, after getting max each time (like sorted desc...): "); while (!maxPQ.IsEmpty()) { Console.Write(maxPQ.DelMax()+" "); } Console.WriteLine(" "); // ------- min priority queue MinPQ<string> minPQ = new MinPQ<string>(11, comparer); minPQ.Insert("S"); minPQ.Insert("T"); minPQ.Insert("R"); minPQ.Insert("P"); minPQ.Insert("N"); minPQ.Insert("O"); minPQ.Insert("A"); minPQ.Insert("E"); minPQ.Insert("I"); minPQ.Insert("H"); minPQ.Insert("G"); Console.WriteLine("Order in binary pyramid: "); foreach (string s in minPQ) { if (s != null) Console.Write(s + " "); } Console.WriteLine(" "); Console.WriteLine("Order, after getting max each time (like sorted asc...): "); while (!minPQ.IsEmpty()) { Console.Write(minPQ.DelMin() + " "); } Console.ReadLine(); } } } |